Решение задач. Экзаменационное задание №6.
07.05.20. Геометрия 10 класс.
Среди задач раздела 6 есть задачи, для решения которых нужно знать свойство медианы прямоугольного треугольника, проведённой из вершины прямого угла
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы.
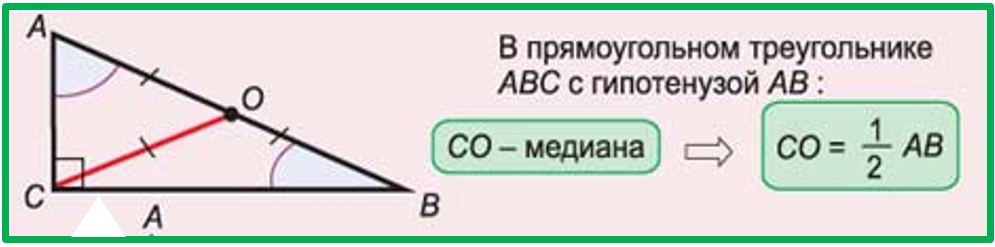
Вспомним, что медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
И эта медиана СО разбивает прямоугольный треугольник на два равнобедренных треугольника: ? АОС и ? ВОС. А в равнобедренных треугольниках углы при основании равны.
Используйте эти свойства треугольников в решении задачи № 1.
В ? АВС ∠В = 40°. Найти углы ? АОС.
Решение.
- Сумма острых углов прямоугольного треугольника равна 90°. значит угол А = 90° - 40° = 50°
- ? АСО равнобедренный, АО = СО, против равных сторон лежат и равные углы, ∠АСО = ∠САО = 50°
- ∠СОА = 180° - (50°+50°) = 80°.
Ответ. Углы ? АСО равны 50°, 50°, 80°.
В задачах 23 и 24 медиана обозначена СD. Для их решения остаточно выполнить действия 1 и 2.
К задачам сделайте чертёж как на таблице.
Домашнее задание: № 23,24

Для отправки ответа преподавателю через "форму отправки ответа" необходимо авторизоваться на сайте (не в консультанте!) с помощью своих логина и пароля полученного при регистрации или по быстрой ссылке отправленной вам на E-Mail. Если вы ещё не заригистрированы на сайте то необходимо пройти одноразовую процедуру регистрации. Читайте: "Как зарегистрироваться на сайте?".
Ответы на E-mail почту или в месенджер "WhatsApp" не принимаются по техническим причинам!
Если не можете войти на сайт, то сообщите о проблеме в онлайн консультант «jivosite». ПАМЯТКА*
Для отправки ответа необходимо авторизоваться!

